A peaceful movement fights against violence and oppression for years, and nothing much changes. Then, everything changes.
Why do many complex systems – cultures, environments, economies – seem stuck (or if good, "stable") despite lots of effort to change them? And why, when change does come, it seems to cascade (or if bad, "collapse") all at once?
There's a tool that can help us understand this:
attractor landscapes. ![]() Or, in less fancy words: "a ball rolling down some hills".
This tool was first created in the field of physics,
but has since been used to help us understand genetics, neuroscience, political alliances, and more!
Or, in less fancy words: "a ball rolling down some hills".
This tool was first created in the field of physics,
but has since been used to help us understand genetics, neuroscience, political alliances, and more!
I'll explain attractors using an environmental example. Let's say you're fishing on a small, sucky pond. You can exhaust your natural resources of fish pretty easily...
Fortunately, fish reproduce, so your population of fish grows back over time. Unfortunately, above some threshold, fish die from overpopulation. And double unfortunately, below some threshold, fish are too sparse to reproduce faster than they die.
Now, let's go fishing, with these forces of growth & death:
If you don't catch too much fish, the ecosystem stays "attracted" to Population=70. You're sustainable! However, catch too much, and the ecosystem's "attracted" to Population=0. You've killed them all!
Nothing much changes. Then, everything changes.
This is why Population=0 and Population=70 are called attractors: because they "attract" the system to it. Likewise, Population=30 is called a repeller, because if the population is slightly below or above 30, it's "repelled" away from 30. Population=30 is also called a tipping point because that's where the ecosystem "tips" from the Population=70 attractor to the Population=0 attractor.
Oof, that's a lot of words.
Wouldn't it be nice to just see how the system behaves at all possible population numbers?
That's where attractor landscapes help!
If we convert the speed of growth/death ![]() into a series of hill slopes
into a series of hill slopes ![]() (faster speeds → steeper slopes) and put a ball
(faster speeds → steeper slopes) and put a ball ![]() on top,
we get something like this:
on top,
we get something like this:
Now, when drawn as a landscape, seeing what the system does is easy!
Mountains ![]() are repellers;
Valleys
are repellers;
Valleys ![]() are attractors.
are attractors.
The depth of a valley is how much energy it takes to escape the attractor. (e.g: Population=0 is deeper than Population=70; that's why it's easier to collapse an ecosystem than to restore it.)
The width of a valley is called the basin of attraction – the range within which the attractor, well, attracts. (e.g: Population=70's basin of attraction is anything within 30<Population≤100)
(Note: our attractor landscape is 2D, because we only have one parameter: Population. If we had more parameters, we could have a 3D landscape, or even a 4D, 5D, or 100D landscape! And at higher dimensions, you can even get what are called strange attractors... but that's for another day.)
In our ball-and-hill metaphor, catching & releasing fish is you trying to move the ball. But what if you could move the hills? In this fishing example, that would mean changing the ecosystem's attractors, by re-introducing predators, increasing plant life, etc.
If you only move the ball, it might just go back to an attractor. But if you move the hills, your changes will stick! You're changing the underlying system itself.
Let's see some not-fishing examples, to show how attractor landscapes really are a powerful way to understand systems. Here's a few from actual academic papers (you can tell they're from academia, because of how Powerpoint-y they look):
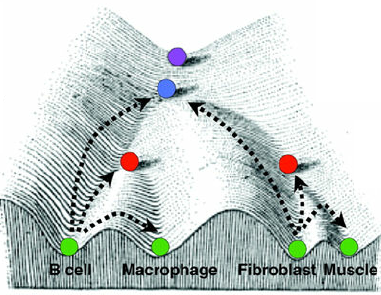 epigenetics: how stem cells become specialized cells
(source)
epigenetics: how stem cells become specialized cells
(source)
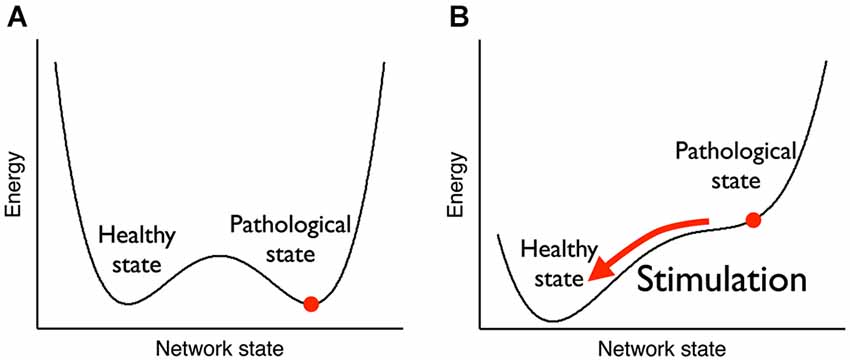 neuroscience: neurological stimulation gets your brain from a stable unhealthy state to a stable healthy state.
(source)
neuroscience: neurological stimulation gets your brain from a stable unhealthy state to a stable healthy state.
(source)
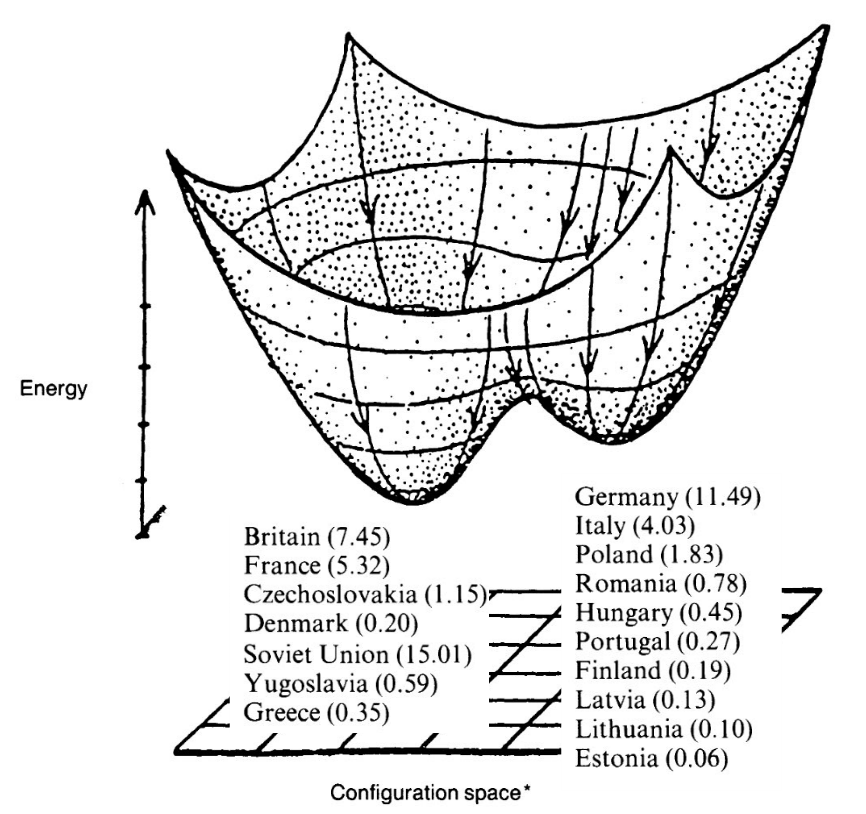 political science: "predicting" likely political alignments during World War II
(source)
political science: "predicting" likely political alignments during World War II
(source)
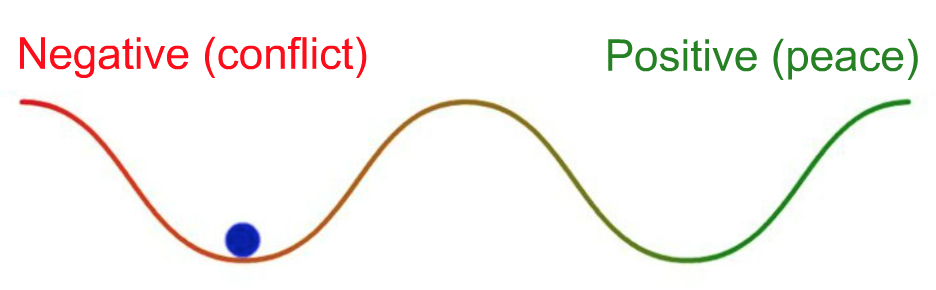 peace studies: peace is not the mere absence of war – they're different attractors!
(source)
peace studies: peace is not the mere absence of war – they're different attractors!
(source)
Finally, let's see our fishing sim again, all together now!
So, the next time you're wondering why things are stuck a certain way, think about:
- What are the "attractors" of this system?
- How "deep" are the valleys? (deeper = harder to escape)
- How "wide" are the valleys? (wider = bigger range of attraction)
- Can we not just move the ball, but move the hills? (changing the underlying system)
And if you ever find yourself frustrated by the world, remember: for many systems, for long periods of time, nothing much changes.
Then, everything changes.